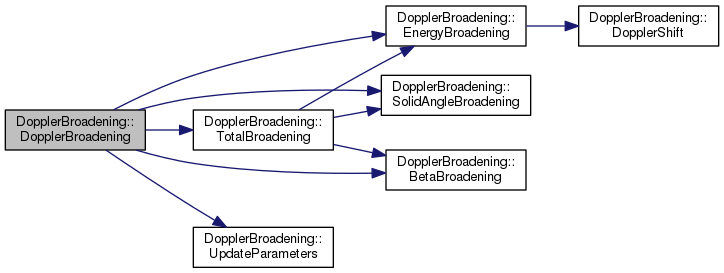
|
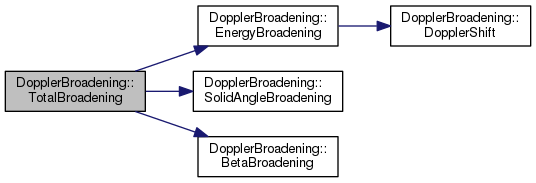
DopplerBroadening
|
|
DopplerBroadening
|
Produces a number of TF1 objects describing the change in energy resolution due to energy shift, opening angle and change in beta value. More...
#include <DopplerBroadening.hpp>
Public Member Functions | |
| DopplerBroadening (const float &energyMeV, const float &beta, const float &dThetaDeg=0, const float &resolutionConst=1, const float &dBeta=0) | |
| Default Constructor. More... | |
| TF1 * | GetEnergyBroadening () |
| Returns a TF1 describing the change in energy resolution due to gamma energy doppler shift. More... | |
| TF1 * | GetSolidAngleBroadening () |
| Returns a TF1 describing the change in energy resolution due to the solid angle coverage of the detector. More... | |
| TF1 * | GetBetaBroadening () |
| Returns a TF1 describing the change in energy resolution due to the distribution of beta values. More... | |
| TF1 * | GetTotalBroadening () |
| Returns a TF1 describing the change in energy resolution due to gamma energy doppler shift, the solid angle coverage of the detector and the distribution of beta values. More... | |
Private Member Functions | |
| void | UpdateParameters () |
| Updates the parameters for each TF1 when called. | |
Static Private Member Functions | |
| static Double_t | DopplerShift (Double_t *ang, Double_t *par) |
| Computes the Doppler shift for the given angle and parameters. More... | |
| static Double_t | EnergyBroadening (Double_t *ang, Double_t *par) |
| Computes the Doppler broadening in resolution for the given angle and parameters. More... | |
| static Double_t | SolidAngleBroadening (Double_t *ang, Double_t *par) |
| Computes the resolution broadening due to opening angle of the detector. More... | |
| static Double_t | BetaBroadening (Double_t *ang, Double_t *par) |
| Returns the total broadening due to energy shift, opening angle and spread in beta values. More... | |
| static Double_t | TotalBroadening (Double_t *ang, Double_t *par) |
| Returns the total broadening due to energy shift, opening angle and spread in beta values. More... | |
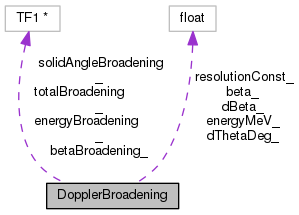
Private Attributes | |
| float | energyMeV_ |
| Energy of the gamma-ray in MeV. | |
| float | beta_ |
| Beta value, ratio of velocity to speed of light. | |
| float | dThetaDeg_ |
| Opening angle of the detector. | |
| float | resolutionConst_ |
Constant term in 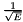 of resolution function. of resolution function. | |
| float | dBeta_ |
| Width of beta distribtuion. | |
| TF1 * | energyBroadening_ |
| Pointer to energy broadening TF1. | |
| TF1 * | solidAngleBroadening_ |
| Pointer to solid angle broadening TF1. | |
| TF1 * | betaBroadening_ |
| Pointer to beta distribution broadening TF1. | |
| TF1 * | totalBroadening_ |
| Pointer to total broadening TF1. | |
Produces a number of TF1 objects describing the change in energy resolution due to energy shift, opening angle and change in beta value.
Doppler broadening is caused by doppler shift of an emitted 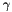 -ray due to a moving frame of reference. This shift is determined by the emitted gamma energy,
-ray due to a moving frame of reference. This shift is determined by the emitted gamma energy, 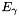 , the speed of the frame of reference written with respect to the speed of light,
, the speed of the frame of reference written with respect to the speed of light, 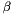 , and the polar angle of the detector relative to the direction of the reference frame,
, and the polar angle of the detector relative to the direction of the reference frame, 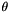 . The detected energy,
. The detected energy, 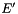 , is then written as
, is then written as
![\[ E' = E_\gamma \frac{\sqrt{1-\beta^2}}{1-\beta cos\theta} \]](form_27.png)
The resolution of a detector is dependent on the energy of the 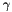 -ray detected. This intrinsic resolution can typically be written as
-ray detected. This intrinsic resolution can typically be written as
![\[ \frac{\delta E_{int}}{E'}(E') = \frac{const.}{\sqrt{E'}} \]](form_45.png)
As the doppler shift causes the 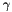 -ray energy to change it adds a broadening to the resolution. The total broadening can then be computed from the intrinsic resolution plus the variance of the doppler shift equation computed via the sum of the partial derivatives squared. For simplification one should divide the broadening by the detected energy giving the following
-ray energy to change it adds a broadening to the resolution. The total broadening can then be computed from the intrinsic resolution plus the variance of the doppler shift equation computed via the sum of the partial derivatives squared. For simplification one should divide the broadening by the detected energy giving the following
![\[ \frac{\delta E'}{E'} = \sqrt{ \left(\frac{\delta E_{int}}{E'}(E')\right)^2 + \left(\frac{\partial E'}{\partial E_\gamma}\frac{\delta E_\gamma}{E'}\right)^2 + \left(\frac{\partial E'}{\partial \theta}\frac{\delta \theta}{E'}\right)^2 + \left(\frac{\partial E'}{\partial \beta}\frac{\delta \beta}{E'}\right)^2 } \]](form_46.png)
Each contribution can be computed separately. The first term from the intrinsic resolution has been explained above. Computing the second term, derivative of the doppler shift equation with respect to the energy of the 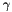 -ray we find
-ray we find
![\[ \frac{\partial E'}{\partial E_\gamma}\frac{\delta E_\gamma}{E'} = \frac{\sqrt{1-\beta^2}}{1-\beta cos\theta}\frac{\delta E_\gamma}{E'} = \frac{\delta E_\gamma}{E_\gamma} \]](form_41.png)
which is simply the uncertainty in the 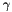 -ray emission.
-ray emission.
The third term, the derivative of the doppler shift with respect to the polar angle can be computed as follows
![\[ \frac{\partial E'}{\partial \theta}\frac{\delta \theta}{E'} = \frac{E_\gamma \beta \sqrt{1-\beta^2} sin\theta} {(1-\beta cos\theta)^2} \frac{\delta \theta}{E'} = \frac{\beta sin\theta}{(1-\beta cos\theta)}\delta \theta \]](form_42.png)
Finally, the fourth term, the derivative of the doppler shift with respect to the beta value can be determined as
![\[ \frac{\partial E'}{\partial \beta}\frac{\delta \beta}{E'} = \frac{E_\gamma |cos\theta - \beta|} {\sqrt{1-\beta^2}(1-\beta cos\theta)^2}\frac{\delta \beta}{E'} = \frac{|cos \theta - \beta|}{(1-\beta^2)(1-\beta cos\theta)}\delta\beta \]](form_43.png)
Definition at line 73 of file DopplerBroadening.hpp.
| DopplerBroadening::DopplerBroadening | ( | const float & | energyMeV, |
| const float & | beta, | ||
| const float & | dThetaDeg = 0, |
||
| const float & | resolutionConst = 1, |
||
| const float & | dBeta = 0 |
||
| ) |
Default Constructor.
Default constructor.
| [in] | energyMeV | The energy of the emitted gamma-ray in MeV. |
| [in] | beta | The fraction of the speed of light of incoming beam. |
| [in] | dThetaDeg | The angular coverage of the detector in degrees. |
| [in] | resolutionConst | The constant term in the 1/sqrt(e) resolution term. |
| [in] | dBeta | The change in beta. |
Definition at line 15 of file DopplerBroadening.cpp.
|
inlinestaticprivate |
Returns the total broadening due to energy shift, opening angle and spread in beta values.
| [in] | ang | The angle value in degrees, index corresponds to power - 1. |
| [in] | par | The parameters of the function. The parameters are:
|
![\[ \frac{\partial E'}{\partial \beta}\frac{\delta\beta}{E'} = \frac{\delta\beta |cos\theta - \beta|}{(1-\beta^2)(1 - \beta cos\theta)} \]](form_44.png)
Definition at line 191 of file DopplerBroadening.hpp.

|
inlinestaticprivate |
Computes the Doppler shift for the given angle and parameters.
| [in] | ang | The angle value in degrees, index corresponds to power - 1. |
| [in] | par | The parameters of the function. The parameters are:
|
![\[ E' = E_\gamma \frac{1-\beta^2}{1-\beta cos\theta} \]](form_17.png)
Definition at line 137 of file DopplerBroadening.hpp.

|
inlinestaticprivate |
Computes the Doppler broadening in resolution for the given angle and parameters.
| [in] | ang | The angle value in degrees, index corresponds to power - 1. |
| [in] | par | The parameters of the function. The parameters are:
|
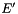 .
.
![\[ \frac{\delta E_{int}}{E'}(E') = \frac{const.}{\sqrt{E'}} \]](form_45.png)
Definition at line 156 of file DopplerBroadening.hpp.


|
inline |
Returns a TF1 describing the change in energy resolution due to the distribution of beta values.
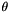 in degrees.
in degrees. Definition at line 102 of file DopplerBroadening.hpp.

|
inline |
Returns a TF1 describing the change in energy resolution due to gamma energy doppler shift.
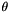 in degrees.
in degrees. Definition at line 88 of file DopplerBroadening.hpp.

|
inline |
Returns a TF1 describing the change in energy resolution due to the solid angle coverage of the detector.
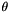 in degrees.
in degrees. Definition at line 95 of file DopplerBroadening.hpp.

|
inline |
Returns a TF1 describing the change in energy resolution due to gamma energy doppler shift, the solid angle coverage of the detector and the distribution of beta values.
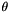 in degrees.
in degrees. Definition at line 110 of file DopplerBroadening.hpp.


|
inlinestaticprivate |
Computes the resolution broadening due to opening angle of the detector.
| [in] | ang | The angle value in degrees, index corresponds to power - 1. |
| [in] | par | The parameters of the function. The parameters are:
|
![\[ \frac{\partial E'}{\partial \theta}\frac{\delta\theta}{E'} = \frac{\beta sin\theta}{1-\beta cos\theta}\delta \theta \]](form_48.png)
Definition at line 173 of file DopplerBroadening.hpp.

|
inlinestaticprivate |
Returns the total broadening due to energy shift, opening angle and spread in beta values.
| [in] | ang | The angle value in degrees, index corresponds to power - 1. |
| [in] | par | The parameters of the function. The parameters are:
|
![\[ \frac{\delta E'}{E'} = \sqrt{ \left(\frac{\delta E_{int}}{E'}(E')\right)^2 + \left(\frac{\partial E'}{\partial \theta}\frac{\delta \theta}{E'}\right)^2 + \left(\frac{\partial E'}{\partial \beta}\frac{\delta \beta}{E'}\right)^2 } \]](form_49.png)
![\[ \left(\frac{\partial E'}{\partial E_\gamma}\frac{\delta E_\gamma}{E'}\right)^2 \]](form_50.png)
Definition at line 221 of file DopplerBroadening.hpp.