|
ReaclibRate
|
|
ReaclibRate
|
A class inheriting from a TF1 that assists in the fitting of a reaction rate to the JINA REACLIB format. More...
#include <ReaclibRate.hpp>
Public Member Functions | |
| ReaclibRate (const char *name, const unsigned int numResonances, const unsigned int z1, const unsigned int z2, const float mu) | |
| Charged particle constructor. More... | |
| void | SetSFactor (const float s0_MeVb) |
| Sets the best guess for the S-factor term S(0). More... | |
| void | SetResonance (const unsigned int resonanceId, const float energy, const float strength) |
| Set parameters for the specified narrow resonance. More... | |
| double | Evaluate (double *t9, double *par) |
| Evaluates the rate at the given temperature and parameters. More... | |
| double | GetSFactor () |
| Returns the S-factor, S(0), determined from the fit parameters. More... | |
| double | GetReducedMass () |
| Returns the reduced mass, determined from the fit parameters. More... | |
| double | GetResonanceEnergy (const unsigned int resosanceId) |
| Returns the resonance energy of the specified resonance set. More... | |
| double | GetResonanceStrength (const unsigned int resosanceId) |
| Returns the resonance strength of the specified resonance set. More... | |
Private Attributes | |
| const unsigned int | numResonances_ |
| The number of resonance sets for this rate. | |
| const unsigned int | z1_ |
| Atomic number of the target. | |
| const unsigned int | z2_ |
| Atomic number of the reactant. | |
| const float | mu_amu_ |
Static Private Attributes | |
| static constexpr float | b_ = 7.8318E9 |
Constant used for non-resonant a0 term. In units of 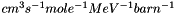 . . | |
| static constexpr float | d_ = 1.5394E11 |
Constant used for resonant a0 term. In units of 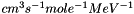 . . | |
A class inheriting from a TF1 that assists in the fitting of a reaction rate to the JINA REACLIB format.
The REACLIB format is a set of seven parameters that provide a functional form for a reaction rate. The expression is designed to provide terms that will fit both non-resonant, charge particle and neutron induced, as well as narrow resonances. This class will take physical parameters (reactant charges, reduced mass, S(0), number of resonances, resonance energies, and resonance strengths) and make educated guess about initial values. After the fit is performed the resulting physical parameters can be extracted.
Definition at line 21 of file ReaclibRate.hpp.
| ReaclibRate::ReaclibRate | ( | const char * | name, |
| const unsigned int | numResonances, | ||
| const unsigned int | z1, | ||
| const unsigned int | z2, | ||
| const float | mu | ||
| ) |
Charged particle constructor.
| [in] | name | The name given to the rate. |
| [in] | numResonances | The number of sets of resonance to add in addition to the non-resonant set. |
| [in] | z1 | The atomic number of the target. |
| [in] | z2 | The atomic number of the reactant. |
| [in] | mu | The reduced mass of the reactants in amu. |
Constructor for charged particle reactions. Specifies the number of resonances as well as the charge and reduced mass of the reactants.
For charged particle reactions the non-resonant set of parameters has a0 fixed based on S(0) (See ReaclibRate::SetSFactor). The a1 term is set based on the charge and mass of the reactants in the following form:
![\[ -4.2486 (Z_1^2 Z_2^2 \mu)^{1/3} \]](form_0.png)
where 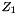 and
and 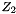 are the charge and
are the charge and 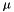 of the reaction reactants. The a3 through a5 terms are allowed to float and the a6 term is set to -2/3.
of the reaction reactants. The a3 through a5 terms are allowed to float and the a6 term is set to -2/3.
For narrow resonances the a0 and a1 term are set based on the resonance energy and strength (See ReaclibRate::SetResonance). The a2 through a5 terms are fixed to 0. Finally, a6 is set to -3/2.
Definition at line 26 of file ReaclibRate.cpp.
| double ReaclibRate::Evaluate | ( | double * | t9, |
| double * | par | ||
| ) |
Evaluates the rate at the given temperature and parameters.
| [in] | t9 | Pointer to T9 values. |
| [in] | par | Pointer to function parameters. |
Evaluates the reaction by summing each set. The zeroth set is the non-resonant term while every additional set are resonant contributions. The terms are evaluated using the following equation:
![\[ \sum_{n}exp\left[ a_{n,0} +\sum_{i=1}^5 a_{n,i} T_9^{2i-5/3} + a_{n,6} \ln T_9 \right] \]](form_12.png)
where 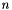 is the set index. Typically a rate has one set for the non-resonant contribution and all subsequent sets are from narrow resonances.
is the set index. Typically a rate has one set for the non-resonant contribution and all subsequent sets are from narrow resonances.
Definition at line 150 of file ReaclibRate.cpp.
| double ReaclibRate::GetReducedMass | ( | ) |
Returns the reduced mass, determined from the fit parameters.
Extracts the reduced mass from the a2 term assuming that Z1 and Z2 are fixed.
Definition at line 109 of file ReaclibRate.cpp.
| double ReaclibRate::GetResonanceEnergy | ( | const unsigned int | resonanceId | ) |
Returns the resonance energy of the specified resonance set.
| [in] | resonanceId | The ID of the resonance to query, starts at 0. |
Extracts the resonance energy from the a1 term of the corresponding resonance set.
Definition at line 124 of file ReaclibRate.cpp.
| double ReaclibRate::GetResonanceStrength | ( | const unsigned int | resonanceId | ) |
Returns the resonance strength of the specified resonance set.
| [in] | resonanceId | The ID of the resonance to query, starts at 0. |
Extracts the resonance strength from the a0 term of the corresponding resonance set using the reduced mass determined from the a2 term of the non-resonant set.
Definition at line 133 of file ReaclibRate.cpp.

| double ReaclibRate::GetSFactor | ( | ) |
Returns the S-factor, S(0), determined from the fit parameters.
Extracts the S-factor term at zero energy, S(0), from the term a0 using the reduced mass determined from a2.
Definition at line 116 of file ReaclibRate.cpp.

| void ReaclibRate::SetResonance | ( | const unsigned int | resonanceId, |
| const float | energy, | ||
| const float | strength | ||
| ) |
Set parameters for the specified narrow resonance.
| [in] | resonanceId | The ID of the associated resonance, begins at 0. |
| [in] | energy | The resonance energy in MeV. |
| [in] | strength | The resonance strength. |
Sets the terms for a resonance set. Specifically, a0 and a1 are set using the resonance strength and energy.
For narrow resonances the a0 term takes on the following form:
![\[ ln[D \mu^{-3/2} \omega\gamma] \]](form_7.png)
where 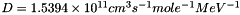 ,
, 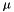 is the reactants reduced mass, and
is the reactants reduced mass, and 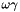 is the narrow resonance strength.
is the narrow resonance strength.
The a1 term takes on the following form:
![\[ -11.6045 E_r \]](form_10.png)
where 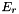 is the resonance energy.
is the resonance energy.
The corresponding parameters are fixed, but can be allowed to float by using the following:
Definition at line 98 of file ReaclibRate.cpp.
| void ReaclibRate::SetSFactor | ( | const float | s0_MeVb | ) |
Sets the best guess for the S-factor term S(0).
| [in] | s0_MeVb | The value for the S-factor in MeV-b at energy zero, S(0). |
Sets the term (a0) of the non-resonant set associated with the s-factor at energy zero, S(0). The a0 term takes the form
![\[ ln[B (Z_1 Z_2 \mu)^{1/3} S(0)] \]](form_4.png)
where 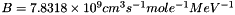 ,
, 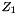 and
and 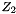 are the charge of the reactants,
are the charge of the reactants, 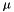 is the reduced mass of the reactants and
is the reduced mass of the reactants and 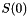 is the value of the S-factor evaluated at an energy of zero.
is the value of the S-factor evaluated at an energy of zero.
The parameter is fixed, but can be allowed to float by using the following:
Definition at line 70 of file ReaclibRate.cpp.
|
private |
Reduced mass of the reactants in amu.
Definition at line 78 of file ReaclibRate.hpp.